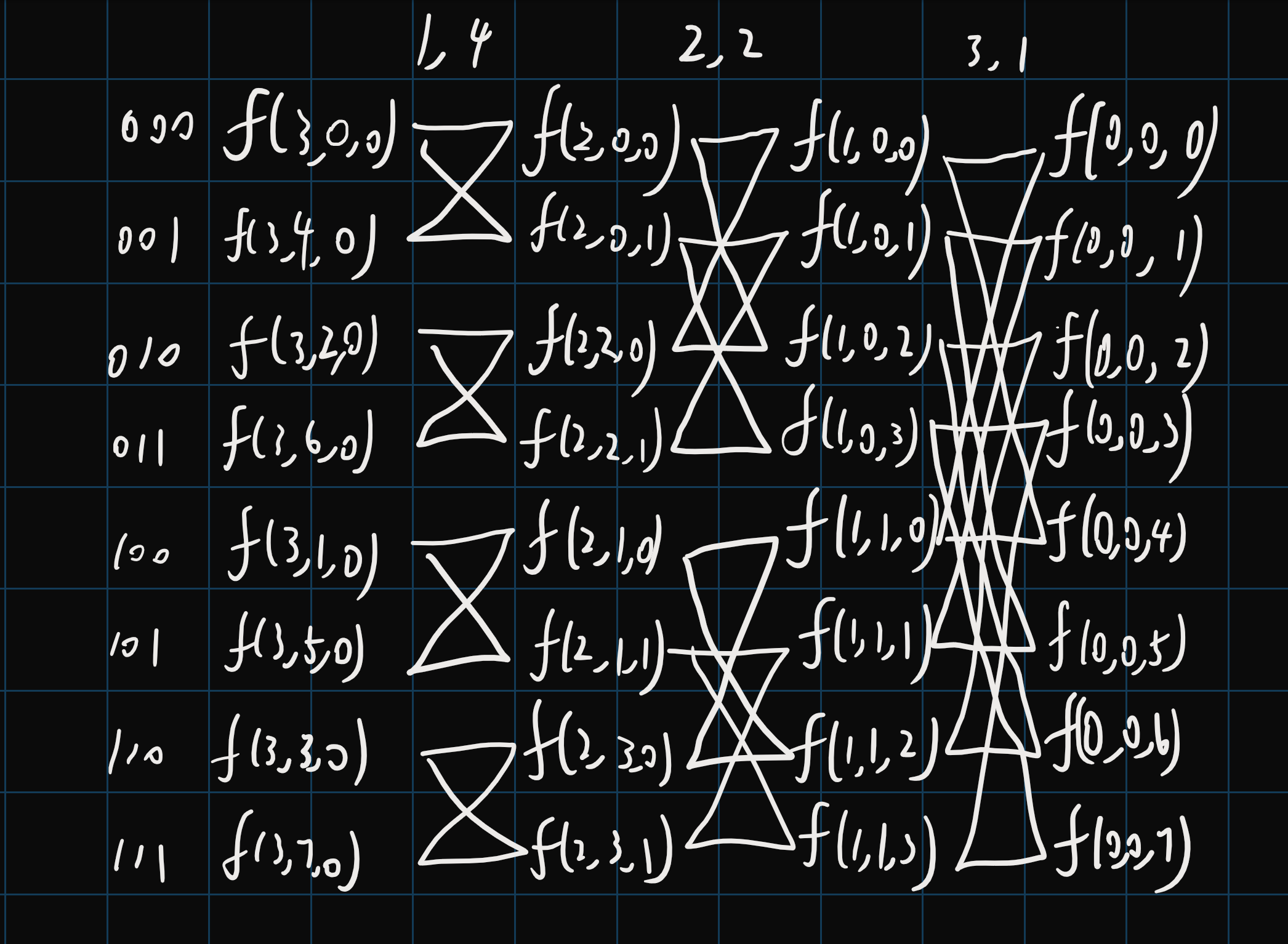Convolution

概念

卷积 (Convolution), 是透过两个函数 $f$ 和 $g$ 生成第三个函数的一种数学算子. ----Wikipedia

上面是卷积的数学定义, 讨论的是连续函数的卷积, 在计算机科学中我们常用的一般的卷积就是对多项式做乘法, 属于离散卷积.

假设我们有两个 $n$ 项的多项式, $f(x) = \sum_{i = 0}^{n - 1}a_ix^i$, $g(x) = \sum_{i = 0}^{n - 1}b_ix^i$. 求两个多项式的差卷积 $\sum_{i = 0}^{2n - 2}\sum_{j = 0}^{i} a_jb_{i - j}x_i$.

常用的离散卷积的计算方法有三种: 直接计算, 分段卷积和快速傅里叶变换.

前两种方法在两个多项式项数相差非常悬殊的时候效率较高, 但是因为最后一种方法在各种情况下都不低, 所以我们主要讨论最后一种.

Fourier transform

傅里叶变换 (Fourier transform) 属于傅里叶分析的领域, 可以将一个函数 $f$ 生成另一个函数 $\hat f$, 记作 $\hat f = \mathcal{F}[f]$. 这个函数的函数值是复数, $\hat f(x)$ 实部虚部分别表示复合信号 $f$ 中, 频率为 $x$ 的信号的振幅和相位.

傅里叶变换是用积分定义的:

$\mathcal{F}[f] (\xi) = \int_{-\infin}^{\infin} f(x)e^{-2\pi ix\xi}dx$

它的逆变换是这样的:

$f(x) = \int_{-\infin}^{\infin} \mathcal{F}[f] (\xi)e^{2\pi ix\xi}d\xi$

对于卷积运算来说, 傅里叶变换的意义在于:

$\mathcal{F}[f * g] = \mathcal{F}[f] \cdot \mathcal{F}[g]$

这样就允许我们把多项式的系数乘法转化为点值乘法, 因为求一个 $n$ 项的多项式的系数, 最少需要 $n$ 个点值. 先求出 $f$, $g$ 的 $O(n)$ 个点值, 然后用 $O(n)$ 的时间算出 $f * g$ 的 $O(n)$ 个点值, 进行傅里叶逆变换即可求出 $f * g$ 的系数表达.

接下来需要解决的就是对 $f$, $g$ 进行傅里叶变换得到 $\mathcal{F}[f]$, $\mathcal{F}[g]$ 的点值, 和对求出的 $\mathcal{F}[f * g]$ 的点值进行傅里叶逆变换 $f * g$ 的过程.

Discrete-time Fourier Transform

离散时间傅里叶变换 (Discrete-time Fourier Transform, DTFT), 指的是在原函数 $f$ 上对时间离散取样 $x_i$, 根据这些 $f(x_i)$, 求出连续函数 $\mathcal{F}[f]$ 的操作.

Discrete Fourier Transform

离散傅里叶变换 (Discrete Fourier Transform, DFT), 则是在离散时间傅里叶变换的基础上, 只求出 $\mathcal{F}[f]$ 的一些点值而不是一个连续的函数.

相比于傅里叶变换中无限的时域, DFT 的时域是 $[0, n)$, 表示离散周期信号的一个周期. $f(j)$ 便是在时间取 $[0, n)$ 中任意整数值的时候, 原信号 $f$ 的点值.

DFT 在傅里叶变换的基础上, 把积分变成了求和. 其中频域也是离散的, 为 $[0, n)$ 内所有的整数, $\mathcal{F}[f] (k)$ 中 $k$ 表示一个周期为单位时间内, 频率为 $k$ 的分量的振幅相位.

$\mathcal{F}[f] (k) = \sum_{j = 0}^{n - 1} e^{-i\frac{2\pi}{n}jk}f(j)$

式子中 $e$ 和 $i$ 分别是自然对数的底数和复数单位, 它们在逆变换的定义式中的意义与之相同.

DFT 的逆变换 IDFT 则被用来根据 $\mathcal{F}[f]$ 的点值求出 $f$ 的点值.

$f(x) = \frac{1}{n} \sum_{j = 0}^{n - 1} e^{i\frac{2\pi}{n}xj}\mathcal{F}[f] (j)$

但是这样求一个点值就需要 $O(n)$ 的时间, 总复杂度就需要 $O(n^2)$. 如何快速求多项式的 DFT 和其逆变换便是我们求多项式乘法的关键.

Euler’s formula

这里的欧拉公式是最优美的那个: $e^{ix} = cos(x) + isin(x)$, 可以通过泰勒级数验证.

这个公式可以理解为用 $e$ 的幂和辐角为 $x$ 的单位复数的关系.

单位根

定义 $n$ 次单位根的 $n$ 次方等于 $1$, 记作 $w_n^k$, 共 $n$ 个. $w_n^k$ 是一个复数, 它的模长为 $1$, 辐角为 $\frac{2\pi k}{n}$, 也就是说, 它是一个单位复数. 用欧拉公式可以表示为:

$w_n^k = e^{\frac{2\pi ki}{n}}$

代入 DFT 的定义式:

$\mathcal{F}[f] (k) = \sum_{j = 0}^{n - 1} w_n^{-jk}f(j)\\ f(j) = \frac{1}{n} \sum_{k = 0}^{n - 1} w_n^{jk}\mathcal{F}[f] (k)$

DFT 和点值

我们前面讨论的 DFT 求的是 $\mathcal{F}[f]$ 的点值, 如果想求 $f$ 的点值, 就需要选择特定的取样点.

如果说我们认为一个多项式 $F(x)$ 是这样的:

$F(x) = \sum_{k = 0}^{n - 1} f(k)x^k$

这时我们取 $x = w_n^{-t}$, 带入这个式子, 发现:

$F(w_n^{-t}) = \sum_{k = 0}^{n - 1} f(k){w_n^{-t}}^k = \sum_{k = 0}^{n - 1} f(k)w_n^{-tk}$

$F(w_n^{-t})$ 的点值不就是 $f(k)$ 的 DFT 吗? 这便是 DFT 和求点值的联系所在. 又因为 $n$ 次单位根的周期性, 我们知道 $w_n^{-t} = w_n^{n - t}$.

$F(w_n^{n - t}) = \mathcal{F}[f] (t) (t \in Z \cup [0, n))\\ F(w_n^{t}) = \mathcal{F}[f] (n - t) (t \in Z \cup [0, n))\\$

这样就可以直接把 DFT 得到的序列作为 $f$ 的点值序列了.

IDFT 和插值

可以用 DFT 的逆变换 (IDFT) 来解决知道 $F$ 在 $w_n^t (t \in Z \cup [0, n))$ 的 $n$ 个点值, 求 $F$ 的系数表示的插值问题.

重新审视 IDFT 的定义式:

$f(j) = \frac{1}{n} \sum_{k = 0}^{n - 1} w_n^{jk}\mathcal{F}[f] (k)$

因为前面推出 $F(w_n^{n - t}) = \mathcal{F}[f] (t) (t \in Z \cup [0, n))$, 代入定义式:

$f(j) = \frac{1}{n} \sum_{k = 0}^{n - 1} w_n^{jk} F(w_n^{n - k})\\ nf(j) = \sum_{k = 0}^{n - 1} w_n^{jk} F(w_n^{n - k})\\ nf(j) = \sum_{k = 0}^{n - 1} w_n^{-jk} F(w_n^{k})\\$

可以用 $F(w_n^k)$ 直接 IDFT 得到 $nf(j)$, 也就是 $F$ 的系数序列的 $n$ 倍.

Fast Fourier Transform

快速傅里叶变换 (Fast Fourier Transform, FFT), 是用来快速计算多项式的离散傅里叶变换和其逆变换的方法.

这里主要研究的是库利-图基 (Cooley-Tukey) 算法. 我们假设 $n$ 是 $2$ 的整数幂, 如果问题中不是, 那么后面的项可以认为是 $0$, 将式子补齐. 这样做不会影响算法复杂度和正确性.

$\begin{aligned} \mathcal{F}[f] (k) &= \sum_{j = 0}^{n - 1} w_n^{-jk}f(j)\\ \mathcal{F}[f] (k) &= \sum_{j = 0}^{\frac n2 - 1} w_n^{-2jk}f(2j) + \sum_{j = 0}^{\frac n2 - 1} w_n^{-(2j + 1)k}f(2j + 1)\\ \mathcal{F}[f] (k) &= \sum_{j = 0}^{\frac n2 - 1} w_{\frac n2}^{-jk}f(2j) + w_n^{n - k} \sum_{j = 0}^{\frac n2 - 1} w_{\frac n2}^{-jk}f(2j + 1)\\ \end{aligned}$

如果这时我们把 $f$ 的偶数项变成 $g(j) = f(2j) (j \in Z \cup [0, \frac n2))$, 奇数项变成 $h(j) = f(2j + 1) (j \in Z \cup [0, \frac n2))$. 那么 $\mathcal{F}[f]$ 就可以用 $\mathcal{F}[g]$ 和 $\mathcal{F}[h]$ 来表示.

当然, $g$ 和 $h$ 的频域可能不包含 $k$, 但是因为离散周期信号是按周期循环的, 所以我们这里的 $k$ 也可以是 $k - \frac n2$.

$\begin{aligned} \mathcal{F}[f] (k) &= \mathcal{F}[g] (k \% \frac n2) + w_n^{n - k} \mathcal{F}[h] (k \% \frac n2)\\ \end{aligned}$

对于只有一个项的序列 $f$, 它的 DFT 可以 $O(1)$ 求出:

$\mathcal{F}[f] (k) = f(0)$

那么我们需要做的就是对于 $n > 1$ 的情况, 递归求解奇数偶数项的 DFT, 然后将它们合并. 第 $x$ 层递归, 有 $2^{\log n - x}$ 个不同的 $k$ 值, 有 $2 ^ x$ 组不同的系数序列. 每次除递归之外的时间复杂度是 $O(1)$, 因此每层的时间复杂度为 $O(n)$. 从一开始的第 $0$ 层开始, 一共是 $\log n + 1$ 层. 因此总复杂度是 $O(n \log n)$.

对于 IDFT, 其原理也是一样的:

$\begin{aligned} f(j) &= \frac{1}{n} \sum_{k = 0}^{n - 1} w_n^{jk}\mathcal{F}[f] (k)\\ nf(j) &= \sum_{k = 0}^{n - 1} w_n^{jk}\mathcal{F}[f] (k)\\ nf(j) &= \sum_{k = 0}^{\frac n2 - 1} w_n^{2jk} \mathcal{F}[f] (2k) + \sum_{k = 0}^{\frac n2 - 1} w_n^{(2k + 1)j} \mathcal{F}[f] (2k + 1)\\ nf(j) &= \sum_{k = 0}^{\frac n2 - 1} w_{\frac n2}^{jk} \mathcal{F}[f] (2k) + w_n^j \sum_{k = 0}^{\frac n2 - 1} w_{\frac n2}^{jk} \mathcal{F}[f] (2k + 1)\\ nf(j) &= \frac n2 g(j \% \frac n2) + w_n^j \frac n2 h(j \% \frac n2) \end{aligned}$

因此其实现和 DFT 是相同的, 只是把 $-w_n$ 变成了 $w_n$, 可以写成一个函数. 复杂度仍然是 $O(n \log n)$. 边界条件:

$f(j) = \mathcal{F}[f] (k)$

因此我们把 $f$ 序列进行 DFT 可以得到 $\mathcal{F}[f]$ 序列, 把 $\mathcal{F}[f]$ 序列进行 DFT 可以得到 $nf$ 序列.

Decimation-in-time

递归毕竟是大常数的写法, 所以实践中尝试用更加方便高效的非递归写法.

定义运算 $Rev_{x}(a)$ 表示把小于 $2^x$ 的数字 $a$ 当成长度为 $x$ 的 01 串, 把这个串镜像过来之后得到的数值大小.

我们知道在 DFT 过程中, 递归时第 $x$ 层有 $2^x$ 个子问题. 回溯时我们需要把第 $x$ 层的第 $j$ 个子问题和第 $j \oplus 2^{x - 1}$ 个子问题合并成第 $x - 1$ 层的第 $j \And (2^{x - 1} - 1)$ 个子问题. 其中, 两个子问题的第 $k$ 项进行操作可以生成新问题的第 $k$ 项和第 $k + 2^{\log n - x}$ 项.

如果想要避免递归, 一个很重要的目标是实现原址操作. 假设一个下标 $j$, 前 $x$ 位从右往左读是 $j_{x, 1}$, 后 $\log n - x$ 位从左往右读是 $j_{x, 2}$ (先读的是高位, 后读的是低位). 如果在第 $\log n$ 层, 使得第 $j$ 位存储第 $j_{x, 1}$ 个子问题的唯一的一项. 如果每一层都能保证第 $j$ 位存储的是第 $j_{x, 1}$ 个子问题的第 $j_{x, 2}$ 项, 并且保证回溯对每两个数进行计算时不会影响其它位置, 就可以通过下标快速计算一些所需的变量, 从而方便地原址求 DFT 了.

利用归纳法, 假设我们在第 $x$ 层满足第 $j$ 位存储的是第 $j_{x, 1}$ 个子问题的第 $j_{x, 2}$ 项, 回溯到第 $x - 1$ 层需要第 $k_1$ 和第 $k_1 \oplus 2^{x - 1}$ 个子问题各自的第 $k_2$ 项相互计算出 $k_1 \And (2^{x - 1} - 1)$ 的第 $k_2$ 项和第 $k_2 + 2^{\log n - x}$ 项.

根据一开始的规定, 第 $x$ 层的第 $k_1$ 个子问题的第 $k_2$ 项的下标是 $2^{\log n - x}Rev_{x}(k_1) + k_2$, 第 $x$ 层的第 $k_1 \oplus 2^{x - 1}$ 个子问题的第 $k_2$ 项的下标是 $2^{\log n - x}Rev_{x}(k_1 \oplus 2^{x - 1}) + k_2$. 变形整理第二个下标:

$\begin{aligned} &2^{\log n - x}Rev_{x}(k_1 \oplus 2^{x - 1}) + k_2\\ = &2^{\log n - x}(Rev_{x}(k_1) \oplus 1) + k_2\\ = &2^{\log n - x}Rev_{x}(k_1) \oplus 2^{\log n - x} + k_2\\ \end{aligned}$

因为 $k_2$ 是第 $x$ 层的子问题中的项, 所以一定小于 $2^{\log n - x}$. 因此:

$\begin{aligned} &2^{\log n - x}Rev_{x}(k_1) \oplus 2^{\log n - x} + k_2\\ = &(2^{\log n - x}Rev_{x}(k_1) + k_2) \oplus 2^{\log n - x}\\ \end{aligned}$

继续变形下标:

$\begin{aligned} &2^{\log n - x}Rev_{x}(k_1) + k_2\\ = &2^{\log n - x}(2Rev_{x - 1}(k_1 \And (2^{x - 1} - 1)) + (\lfloor \frac {k_1}{2^{x - 1}} \rfloor \And 1)) + k_2\\ = &2^{\log n - x + 1}Rev_{x - 1}(k_1 \And (2^{x - 1} - 1)) + 2^{\log n - x}(\lfloor \frac {k_1}{2^{x - 1}} \rfloor \And 1) + k_2\\ &2^{\log n - x}Rev_{x}(k_1 \oplus 2^{x - 1}) + k_2\\ = &(2^{\log n - x}Rev_{x}(k_1) + k_2) \oplus 2^{\log n - x}\\ = &(2^{\log n - x + 1}Rev_{x - 1}(k_1 \And (2^{x - 1} - 1)) + 2^{\log n - x}(\lfloor \frac {k_1}{2^{x - 1}} \rfloor \And 1) + k_2) \oplus 2^{\log n - x}\\ = &2^{\log n - x + 1}Rev_{x - 1}(k_1 \And (2^{x - 1} - 1)) + 2^{\log n - x}(\lfloor \frac {k_1}{2^{x - 1}} \rfloor \And 1) \oplus 2^{\log n - x} + k_2\\ \end{aligned}$

因此这两个下标是计划中第 $x - 1$ 层的第 $k_1 \And (2^{x - 1} - 1)$ 个子问题的第 $k_2$ 和 $k_2 + 2^{\log n - x}$ 项, 因此可以保持原址操作.

对于长度为 $8$ 的序列, 其过程如图所示, 图中 $f(a, b, c)$ 表示第 $a$ 层回溯时, 第 $b$ 个子问题的第 $c$ 项:

因为这个过程的输入是信号, 是在时域的每个点取样, 所以又叫时域抽取法 (Decimation-in-time, DIT). 使用 DIT 时需要先把变换序列的第 $j$ 项赋值为原信号的第 $Rev_{\log n}(j)$ 项, 最后变换得到的结果序列中 $j$ 位置存储的则是频谱中的第 $j$ 项.

下面是 DIT 实现的库利-图基算法的代码, 其中 Cplx(x) 表示 $w_n$ 或 $-w_n$ 的 $x$ 次方, 如果是 DFT 则是 $-w_n$, 否则是 $w_n$.

1
2
3
4
5
6
7
8
9

inline void DIT(Cplx* f) {
  for (unsigned i(Lgn), j(1); i; --i, j <<= 1) {
    for (unsigned k(0); k < n; ++k) if (!(k & j)) {
      Cplx Tma(f[k]), Tmb(f[k + j]), W(Cplx((k & ((j << 1) - 1)) << (i - 1)) * Tmb);
      f[k] = Tma + W;
      f[k + j] = Tma - W;
    }
  }
}

Decimation-in-frequency

DIT 需要把信号以二进制镜像的下标存储, 我们如果仅使用 DIT, 那么一次多项式乘法就需要进行 $3$ 次转置 (输入的两个序列的转置和点值乘法后的转置), 这无疑是没有必要的. 如果考虑逆过程, 直接把频谱扔进一个函数, 得到的是转置后的信号, 和 DIT 同时使用就可以完全避免转置.

与 DIT 相对的, 频域抽取法 (Decimation-in-frequency, DIF), 是前者的逆过程, 它模拟的是 DIT 的逆过程.

已知

$\mathcal{F}[f] (k) = \mathcal{F}[g] (k \% \frac n2) + w_n^{n - k} \mathcal{F}[h] (k \% \frac n2)\\$

如果已知 $\mathcal{F}[f]$, 求 $\mathcal{F}[g]$ 和 $\mathcal{F}[h]$.

$\begin{aligned} 2\mathcal{F}[g] (k) &= \mathcal{F}[g] (k) + w_n^{n - k} \mathcal{F}[h] (k) + \mathcal{F}[g] (k) - w_n^{n - k} \mathcal{F}[h] (k)\\ &= \mathcal{F}[g] (k) + w_n^{n - k} \mathcal{F}[h] (k) + \mathcal{F}[g] (k) + w_n^{n - k - \frac n2} \mathcal{F}[h] (k)\\ &= \mathcal{F}[f] (k) + \mathcal{F}[f] (k + \frac n2)\\ 2w_n^{n - k}\mathcal{F}[h] (k) &= \mathcal{F}[g] (k) + w_n^{n - k} \mathcal{F}[h] (k) - \mathcal{F}[g] (k) + w_n^{n - k} \mathcal{F}[h] (k)\\ &= \mathcal{F}[g] (k) + w_n^{n - k} \mathcal{F}[h] (k) - \mathcal{F}[g] (k) - w_n^{n - k - \frac n2} \mathcal{F}[h] (k)\\ &= \mathcal{F}[f] (k) - \mathcal{F}[f] (k + \frac n2)\\ 2\mathcal{F}[h] (k) &= w_n^{k} (\mathcal{F}[f] (k) - \mathcal{F}[f] (k + \frac n2)) \end{aligned}$

因此直接把频谱喂给 DIF 实现的库利-图基算法, 就可以得到 $n$ 倍的原信号转置后的序列. 因为输入是频谱, 定义在频域上, 所以称为频域抽取法下面是代码.

1
2
3
4
5
6
7
8
9

inline void DIF(Cplx* f) {
  for (unsigned i(1), j(n >> 1); i <= Lgn; ++i, j >>= 1) {
    for (unsigned k(0); k < n; ++k) if (!(k & j)) {
      Cplx Tma(f[k]), Tmb(f[k + j]);
      f[k] = Tma + Tmb;
      f[k + j] = (Tma - Tmb) * Cplx((k & (j - 1)) << (i - 1));
    }
  }
}

代码的剩余部分

由于是复数操作, 所以我们首先定义一个复数类.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

double Cp[2100000][2];
unsigned m, n, nn, Lgn(0);
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(1);
char Inv(0);
struct Cplx {
  double Rel, Img;
  inline Cplx() {}
  inline Cplx(unsigned x) {
    Rel = Cp[x][0]; Img = Inv ? Cp[x][1] : -Cp[x][1];
  }
  inline Cplx operator + (const Cplx& x) {
    Cplx Rt(x);
    Rt.Rel += Rel, Rt.Img += Img;
    return Rt;
  }
  inline Cplx operator + (const double& x) {
    Cplx Rt(*this);
    Rt.Rel += x, Rt.Img;
    return Rt;
  }
  inline Cplx operator - (const Cplx& x) {
    Cplx Rt(x);
    Rt.Rel = Rel - Rt.Rel, Rt.Img = Img - Rt.Img;
    return Rt;
  }
  inline Cplx operator - (const double& x) {
    Cplx Rt(*this);
    Rt.Rel -= x, Rt.Img;
    return Rt;
  }
  inline Cplx operator * (const Cplx& x) {
    Cplx Rt;
    Rt.Rel = Rel * x.Rel - Img * x.Img, Rt.Img = Img * x.Rel + Rel * x.Img;
    return Rt;
  }
  inline Cplx operator * (const double& x) {
    Cplx Rt(*this);
    Rt.Rel *= x, Rt.Img *= x;
    return Rt;
  }
  inline Cplx operator / (const Cplx& x) {
    Cplx Rt;
    double TmpDe(x.Rel * x.Rel + x.Img * x.Img);
    Rt.Rel = (Rel * x.Rel + Img * x.Img) / TmpDe;
    Rt.Img = (Img * x.Rel - Rel * x.Img) / TmpDe;
    return Rt;
  }
  inline Cplx operator / (const double& x) {
    Cplx Rt(*this);
    Rt.Rel /= x, Rt.Img /= x;
    return Rt;
  }
}a[2100000], b[2100000];

然后是主函数. 我们用 DIF 求出两个输入信号的频谱的转置, 然后用 DIT 求出转置的频谱相乘得到的结果的原信号增强 $n$ 倍的结果.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

signed main() {
  nn = RD() + 1, m = RD() + 1, n = nn + m - 1;
  while (Tmp < n) Tmp <<= 1, ++Lgn; n = Tmp;
  for (unsigned i(0); i <= n; ++i) {//预处理 n 次单位根
    double Arc(Pi * 2 * i / n);
    Cp[i][0] = cos(Arc), Cp[i][1] = sin(Arc);
  }
  for (unsigned i(0); i < nn; ++i) a[i].Rel = RD();
  for (unsigned i(0); i < m; ++i) b[i].Rel = RD();
  DIF(a), DIF(b);//正变换
  for (unsigned i(0); i < n; ++i) a[i] = a[i] * b[i];
  Inv = 1, DIT(a);//逆变换
  for (unsigned i(0); i < n; ++i) a[i] = a[i] / n;//逆变换让值增加到原来的 n 倍
  for (unsigned i(0); i < m + nn - 1; ++i) printf("%u ", (unsigned)(a[i].Rel + 0.5));putchar(0x0A);
  return Wild_Donkey;
}

Prime Root

假设 $a$, $m$ 互质, 我们知道 $a^d \equiv a^{d \% \phi(m)} \pmod m$, 因此任何整数 $a$ 在模 $m$ 意义下的整数幂的结果, 只有 $\phi(m)$ 种.

如果对于正整数 $a$, 使得 $a^d \equiv 1 \pmod m$ 成立的最小的正整数 $d$ 等于 $\phi(m)$. 则称 $a$ 是模 $m$ 的一个原根 (Prime Root).

如果 $m$ 可以用正整数 $n$ 和奇质数 $p$ 表示为 $p^n$ 或 $2p^n$, 又或是 $m = 2$ 或 $m = 4$, 则存在模 $m$ 的原根.

通过有关群论的知识我们知道, 如果一个数 $m$ 有原根, 那么它的不同的原根数量为 $\phi(\phi(m))$.

Number-Theoretic Transform

数论变换 (Number-Theoretic Transform, NTT), 是用原根代替 $n$ 次单位根以避免复数运算的处理整数离散周期信号的算法.

仍然是把原来的序列加 $0$ 补齐为长度为 $2$ 的整数幂的序列, 长度为 $n$. 我们选择一个质数 $m$ 作为模数, 需要满足 $n | m - 1$, 找出模 $m$ 的一个原根 $\alpha$, 把 $\alpha^{\frac {m - 1}n} \pmod m$ 记作 $w_n$.

NTT 的定义式和 DFT 的定义式形式上十分相似, 如果没有说明, 我们下面提到的所有运算都是模 $m$ 意义下的, 用 $Inv(x)$ 表示 $x$ 模 $m$ 意义下的乘法逆元.

$F(k) = \sum_{j = 0}^{n - 1} w_n^{jk}f(j)\\ f(j) = Inv(n)\sum_{k = 0}^{n - 1} w_n^{-jk}F(k)$

先来看正变换:

$\begin{aligned} F(k) &= \sum_{j = 0}^{n - 1} w_n^{jk}f(j)\\ &= \sum_{j = 0}^{\frac n2 - 1} w_n^{2jk}f(2j) + \sum_{j = 0}^{\frac n2 - 1} w_n^{(2j + 1)k}f(2j + 1)\\ &= \sum_{j = 0}^{\frac n2 - 1} w_{\frac n2}^{jk}f(2j) + w_n^k \sum_{j = 0}^{\frac n2 - 1} w_{\frac n2}^{jk}f(2j + 1)\\ &= G(k) + w_n^k H(k)\\ \end{aligned}$

然后是逆变换:

$\begin{aligned} f(j) &= Inv(n)\sum_{k = 0}^{n - 1} w_n^{-jk}F(k)\\ nf(j) &= \sum_{k = 0}^{n - 1} w_n^{-jk}F(k)\\ nf(j) &= \sum_{k = 0}^{\frac n2- 1} w_n^{-2jk}F(2k) + \sum_{k = 0}^{\frac n2- 1} w_n^{-(2k + 1)j}F(2k + 1)\\ nf(j) &= \sum_{k = 0}^{\frac n2- 1} w_{\frac n2}^{-jk}F(2k) + w_n^{-j} \sum_{k = 0}^{\frac n2- 1} w_{\frac n2}^{-kj}F(2k + 1)\\ nf(j) &= \frac n2 G(j) + w_n^{-j} \frac n2 H(j)\\ \end{aligned}$

发现式子可以直接使用库利-图基算法求, 其流程和复数实现的 DFT 是一样的.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

const unsigned long long Mod(998244353);
unsigned long long W, a[2100000], b[2100000];
unsigned m, n, nn, Lgn(0);
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(1);
char Inv(0);
inline unsigned long long Pow(unsigned long long x, unsigned y) {
  unsigned long long PR(1);
  while (y) {
    if (y & 1) PR = PR * x % Mod;
    x = x * x % Mod, y >>= 1;
  }
  return PR;
}
inline void DIT(unsigned long long* f) {
  for (unsigned i(1), j(Lgn - 1); ~j; --j, i <<= 1) {
    unsigned long long Pri(Pow(Inv ? W : Pow(W, Mod - 2), 1 << j)), Po(1);
    for (unsigned k(0); k < n; ++k, Po = Po * Pri % Mod) if (!(k & i)) {
      unsigned long long Tma(f[k]), Tmb(f[k + i] * Po % Mod);
      f[k] = Tma + Tmb;
      f[k + i] = Mod + Tma - Tmb;
      if (f[k] >= Mod) f[k] -= Mod;
      if (f[k + i] >= Mod) f[k + i] -= Mod;
    }
  }
}
inline void DIF(unsigned long long* f) {
  for (unsigned i(n >> 1), j(0); i; ++j, i >>= 1) {
    unsigned long long Pri(Pow(Inv ? W : Pow(W, Mod - 2), 1 << j)), Po(1);
    for (unsigned k(0); k < n; ++k, Po = Po * Pri % Mod) if (!(k & i)) {
      unsigned long long Tma(f[k]), Tmb(f[k + i]);
      f[k] = Tma + Tmb;
      if (f[k] >= Mod) f[k] -= Mod;
      f[k + i] = (Mod + Tma - Tmb) * Po % Mod;
    }
  }
}
signed main() {
  nn = RD() + 1, m = RD() + 1, n = nn + m - 1;
  while (Tmp < n) Tmp <<= 1, ++Lgn; n = Tmp;
  W = Pow(3, (Mod - 1) / n);
  for (unsigned i(0); i < nn; ++i) a[i] = RD();
  for (unsigned i(0); i < m; ++i) b[i] = RD();
  DIF(a), DIF(b);
  for (unsigned i(0); i < n; ++i) a[i] = a[i] * b[i] % Mod;
  Inv = 1, DIT(a), W = Pow(n, Mod - 2);
  for (unsigned i(0); i < n; ++i) a[i] = a[i] * W % Mod;
  for (unsigned i(0); i < m + nn - 1; ++i) printf("%llu ", a[i]); putchar(0x0A);
  system("pause");
  return Wild_Donkey;
}

总结

综合前面两种计算卷积的方法的共同点, 只要一个数 $\alpha$ 符合下面的条件, 都可以用来作为 DFT 计算卷积的旋转因子, 而 $-\alpha$ 则被作为是 IDFT 过程的旋转因子:

• $\alpha^{2^k} = 1$

• $\alpha^{j + 2^{k - 1}} = -\alpha^{j}$

值得注意的是, 只有 $-w_n$ 可以用来将信号转化为频谱, 其它的 $\alpha$ 都只能用于计算卷积.